• home
• writing
• research

Models of synaptic conductance III

NOTE  In this set of articles I would like to cover three simple models of synaptic conductance which are typically used in spiking networks. While people are quite familiar with their general logic, the exact mathematical details are often overlooked or simply swept under the rug because they are deemed too simple. I will take on this all-too-simple task, and talk about the mathematical ideas behind these basic models.

So far in this series, we have looked at ISED and Alpha synapses. While the ISED model completely forgoes the time-course of the onset of the transfer function, the Alpha model represents it symmetrically, with equal rise and fall time-constants. However, most neurotransmitters show rapid release dynamics and sustained synaptic currents, thus calling for a more unsymmetrical representation of the onset and decay dynamics. In this third and final article of the series we will look at one such model - the bi-exponential synapse.

This model can be viewed as an extension of the Alpha synapse. The transfer function at the bi-exponential synapse can be written as:

Here, is the conductance over time, is the maximum amplitude, is a normalisation constant, is the decay time-constant, and is a parameter which describes how the rise-time is related to the decay-time. This formulation is not very common and usually models tend to use a second time constant instead of the parameter . However, in my work I have found that is not very intuitive to interpret and we will use the parameter instead.

We will begin with two remarks about equation . First, the constant is calculated such that . Second this maxima occurs at given by:

Thus, the parameter is the time-to-peak of the transfer function, and the parameter , in some sense, is a measure of how the rise-time of the transfer function relates to its decay-time . This is shown in the figure below.

Note that the relationship is supra-linear, and since we have restricted , the rise-time cannot exceed the decay-time. How does this synapse react to an input spike though? Below, I show the impulse response of a bi-exponential synapse.

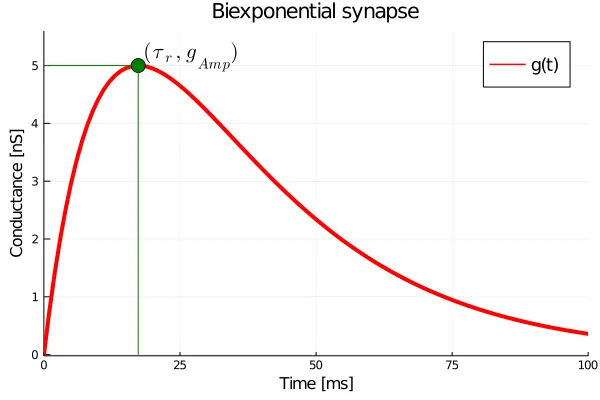
Here, we have set , , and . Using equation we see that the rise-time comes to about . Let us look a the trajectories of motion of this system. From our experience with Alpha synapses we know that we will need at least two variables to describe the state. After some work we will arrive at the system given by:

Here, is the conductance over time and is a hidden variable. The behaviour of the system starting from an initial conductance of is shown below. Only the ‘real-world’ first and third quadrants are plotted.

Some more analysis reveals that the system has a degenerate node at the origin (black dot). The sense of all trajectories is towards this fixed point. Let us focus on the green trajectory defined by . Along this trajectory, the conductance increases till it reaches a maximum amplitude of , before going down to again. Just as in the Alpha synapse, this amplitude is equal to the initial value of the state variable , i.e., . However, unlike the Alpha synapse the onset and the decay are not symmetrical. While the onset is parallel to the faster eigendirection of the system (red dashed line), the subsequent decay towards the degenerate node, as expected, follows the slower eigendirection (blue dashed line). To incorporate spiking behaviour in the system, it suffices to make a simple adjustment to equation :

Here, the pre-synaptic spike (arriving at ) leads to an eventual increase in the conductance by . Like the Alpha synapse, the jump is instantaneous in , but its effect on the conductance is reflected in a smooth increase which peaks at . This ‘hop’ moves the system to a different trajectory and the input pulses are treated additively. The figure below shows this system under a volley of input spikes with amplitudes between and , delivered irregularly. The arrival times of the input spikes are marked with grey vertical lines.

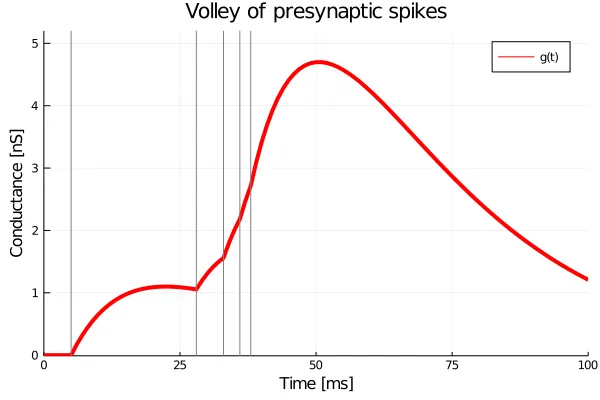
Since the interval between the first two spikes is rather large, the conductance reaches a maximum and then begins to dip. The final four spikes, on the other hand, are very close to each other, and all we see is a steady rise in conductance.

In my experience, bi-exponential synapses have little to offer over Alpha synapses in most models. However, there are several situations where these synapses can be very useful - e.g., models which explore the effects of heterogeneity, models which capture inter-population interactions, and of course, models which explore sub- dynamics.